DEVRE ELEMANI OLARAK DİYOT
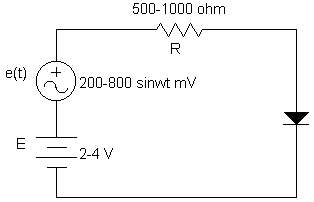
Elektronik devre bileşenleri genellikle 'küçük sinyal' ve 'büyük sinyal' olmak üzere iki farklı uygulama ile çalıştırılırlar. Küçük sinyal uygulamalarında, I-V karakteristik eğrisinin çok sınırlı bir aralığında akım ve gerilim değişimi olur. Diğer bir ifadeyle, DV ve DI değerleri, devre bileşeninin çalışma bölgesindeki gerilim ve akım aralığı ile karşılaştırıldığında çok küçüktür. Bunun aksine büyük-sinyal çalışması devre bileşeninin I-V karakteristik eğrisinin büyük ölçüde tüm aralığında meydana gelmektedir. Şeki-3'de ki devre bir dc gerilim kaynağı ve buna seri bir ac gerilim kaynağı içermektedir. dc gerilim kaynağı sabit E volt kadar gerilim üretir, ve ac gerilim kaynağı e = Asinwt sinus dalgası üretir. Burada tepe değeri A'nın E'ye göre çok küçük olduğu varsayılır. Seri direnç ve diyot devresine toplam E + Asinwt kadar gerilim uygulanmaktadır. Toplam gerilim n(t) E kadar dc seviyeli bir ac gerilim olarak adlandırılır. n(t) maksimum E + A ve minimum E - A kadardır. Bu durumda belirlenmek istenen, küçük-sinyal çalışma için yeterli küçüklükteki diyot gerilimi ve akımıdır.
Böyle bir devrenin elektriksel olarak süperpozisyon (superposition) tekniği kullanılarak çözülmesi mümkündür. Devre akımı her bir kaynağın devreye tek başına etkisi hesap edilerek belirlenebilir. Süperpozisyon tekniği yalnızca tüm devre bileşenleri doğrusal olduğunda uygulanabilir. Küçük-sinyal çalışması uygulaması yapıldığından burada bir sorun söz konusudur. Öncelikle dc diyot akımı tespit edilmelidir, böylece diyotun ac direnci(rd) hesaplanabilir. Önceki bölümden diyotun dc devrede kullanılması durumunda üzerine düşen gerilimin sabit 0.7V olarak kabul edildiğini biliyoruz. Böylece dc devre akımı:
Ardından,
diyotun ac direnci hesaplanır.
Devreden dc kaynağı kaldırıp yerine ac kaynağı bağlayacak olursak diyot burada bir önceki adımda tespit edilen rd ohm kadar değere sahip bir direnç gibi davranır. Devrenin ac eşdeğer devresinde diyot yerine rd ohm kadar değerde bir direnç kullanılır. Devrenin ac akımı:
ac diyot gerilimi nD ise nD = ird denkleminden hesaplanabilir. dc ve ac analizlerden elde edilen sonuçları birleştirmek suretiyle diyottaki toplam akım ve gerilimi aşağıdaki denklemlerle gösterebiliriz:
nD(t) = 0.7 + rdAsinwt /(R + rd). III Aşağıdaki aplette silikon bir diyodun Şekil-3'te ki devre örnek alınmak suretiyle küçük sinyal uygulamasında çalıştırılması gösterilmiştir. Devreden geçen akımın durumunu, devredeki gerilim kaynaklarının ve direncin değerlerini belli sınırlar arasında değiştirmek suretiyle izleyebilirsiniz. Bu devrenin DC yük eğrisi, I = (E- VD)/R, denklemiyle bulunur. Burada -1/R DC yük eğrisinin eğimidir.
|