DEVRE ELEMANI OLARAK DİYOT

[Diyotlu DC Devrelerin Analizi] [Küçük-Sinyal Devre Analizi] [Büyük-Sinyal Devre Analizi-1] [Büyük-Sinyal Devre Analizi-2] [Zener Diyot]
Giriş:
[-Ana Sayfa-] [İleri>>>]

Doğrusal Olmayan Devre Elemanı Olarak Diyot:

İçerisinden geçen akıma karşın üzerinde oluşan gerilime ilişkin grafiğinin eğimi her noktada sabit olan devre bileşeni doğrusal bir devre elemanı olarak adlandırılır. Eğer ölçülen gerilim ve buna karşılık gelen akım değerlerine sahipsek bu değerleri kullanmak suretiyle çizilen grafikten doğrusallığın olup olmadığı tespit edilir.
Aşağıda bir devre bileşeni üzerindeki akım ve gerilim ilişkisi gösterilmiştir:

V=K1I + K2 I
I = K'1V + K'2 II

Burada K1, K2, K'1 ve K'2 herhangi sabitlerdir. I. denklemde  K1 doğrunun eğimidir ve birimi ohm'dur.  Denklem-2'de K'1 eğimdir ve birimi siemens (mho) 'dur.

Temel devre analizlerinden bildiğimiz üzere direnç, kapasitör ve endüktörler doğrusal elektronik bileşenlerdir. Çünkü herbirinin sahip olduğu gerilim-akım denklemi  K2 0'a eşit olmak üzere I. denklemin formundadır.

  • Direnç için R, V = IR; K1 = R,
  • Kapasitans için C, V = IXc; K1 = Xc (kapasitif reaktans),
  • Endüktans için L, V = IXL ; K1 = XL (endüktif raktans)'dır.

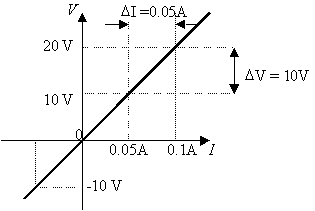
Şekil-1'de doğrusal bir devre elemanı olan 200ohm'luk bir dirence ait akım-gerilim eğrisi gösterilmektedir. Dikey eksen direnç üzerindeki gerilimi yatay eksen dirençten geçen akımı göstermektedir. Böylece r = DV/ DI = 200ohm eşitliği sağlanmaktadır. Dikkat edilirse her noktada eğim aynı olduğundan direnç değeri de sabittir .

Şekil-1

Ancak diyot denklemi aşağıdaki gibidir;
I = Is(eV/nVT - 1)
Burada;
Is = saturasyon akımı
VT = termal gerilim
n = değeri 1 ile 2 arasında değişen, V'nin bir fonksiyonudur.

Denklemden açıkça görüleceği üzere diyotun gerilim-akım ilişkisi bir doğrusal elektronik bileşen için gereken şartı karşılamamaktadır. Bu nedenle diyot için bir nonlinear (doğrusal olmayan) bileşen ifadesi kullanılır.

Şekil-2 DV ve DI değerlerinin I-V eğrisi üzerinde nasıl iki farklı noktada bulunduğunu göstermektedir. Bu değerleri kullanarak diyotun direncini  r = DV/ DI denkleminden hesaplayabiliriz. V = 0.65V ve I = 30mA olduğu noktada

r = DV/ DI = 0.015V / (20 x 10-3)A = 0.75ohm

V = 0.58V ve I = 2.2 mA olduğu noktada,

r = DV/ DI = 0.04V / (4x10-3)A = 10ohm'dur.

Burada görüldüğü üzere doğrusal bir devre bileşeninden farklı olarak 10 katlık bir değişimden daha fazla değişim söz konusudur. Diyotun ters kutuplandığı bölgede gerilime karşın akım değişimi neredeyse hiç yoktur. Bu bölgede diyot direnci çok büyüktür. Yüksek dirençten alçak dirence geçiş bölgesi dirsek noktası olarak adlandırılır.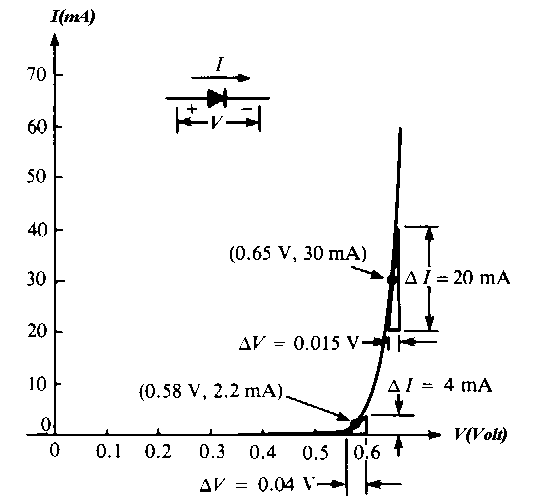

Şekil-2

AC ve DC Diyot Direnci

Önceki bölümde DV/DI denklemini kullanarak hesapladığımız direnç diyodun 'dinamik direnci (ac direnç)' olarak adlandırılır. Diyodun ac direnci için, diyodun üzerine düşen gerilimin anlık değer farklarının meydana getirdiği akım değişiminin bir sonucu olarak ortaya çıktığı söylenebilir. Denklemlerde diyodun ac direncini göstermek amacıyla 'rd' kısaltması kullanılmaktadır. Diyoda dc bir gerilim uygulandığında içerisinden belli bir akım geçecektir. Diyodun dc direnci, o an üzerine düşen gerilimin içinden geçen akıma oranı olarak bulunur. Diyodun dc direnci 'RD' kısaltmasıyla gösterilir.

    DC diyot direnci RD = V/I ohm olarak ifade edilir.

Örnek Uygulama Apleti

Aşağıdaki aplette belli bir diyodun gerilim ve akım ilişkisi gösterilmiştir. Bu amaçla ayarlanabilir bir direnç diyoda seri bağlanmıştır. Sabit 5 Voltluk bir gerilim kaynağı devreye uygulanmıştır. Ayarlanabilir direnç yardımıyla diyot akımı kontrol edilmektedir. Ayarlanabilir direncin belli değer aralıklarında diyot üzerindeki gerilim sabit kalmakta bu aralıkların dışında değişmektedir. Bu örnekte devreden geçen akım, belli direnç aralığındaki diyot gerilimi, diyodun dc ve ac dirençleri hesaplanmaktadır. Örneğin:

    6.3 k'lık ayarlanabilir direncin 6.3k ile 4.2k aralığında diyot üzerindeki gerilim 0.55V'tur, direncin 6.3k olduğu durumda devre akımı;
    I1 = (5 -0.55)/6.3k = 0.705 mA olarak bulunur,
    diyodun bu durumdaki dc direnci;
    RD = 0.55/0.705m = 780ohm olarak bulunur.

    Eğer ayarlanabilir direnç değeri 4.2k'ya düşürülecek olursa diyot üzerindeki gerilim 0.56V'a çıkar ve bu durumda 0.56V ile 0.55V aralığındaki ac direnci hesaplayabiliriz; 

    I2 = (5 - 0.56)/4.2k = 1.05mA, öyleyse bu noktadaki ac diyot direnci;

    rd = (0.56 - 0.55)/(1.05 - 0.705)m = 29 ohm olarak bulunur.

    Yaklaşık diyot ac direnci termal gerilimin ( oda sıcaklığında 0.026V'tur) akıma oranıyla da hesaplanabilir.

    rd = 0.026/I

Bu bölümde JAVA Apleti vardır. Apleti oynatabilmek için Google Chrome Tarayıcınızın "Extensions" kısmından CheerpJ eklentisinin çalıştırılması gerekir.

[-CheerpJ Applet Runner -]

[Free Source Code]
[-Ana Sayfa-] [İleri>>>]